Liên hệ quảng cáo
Phương pháp tính tấm chữ nhật chịu uốn có xét biến dạng trượt ngang sử dụng nội lực làm ẩn
Bài báo trình bày phương pháp sử dụng nội lực (mô men uốn Mx, My, mô men xoắn Mxy, lực cắt Qx, Qy) làm ẩn và nguyên lý năng lượng biến dạng đàn hồi tối thiểu để xây dựng bài toán tấm chịu uốn khi có xét biến dạng trượt ngang, sau đó đưa ra một ví dụ lời giải số và so sánh kết quả với lời giải giải tích.
|
ª ThS. NCS. Mai Thị Hải Vân ª TS. Đỗ Ngọc Viện Trường Đại học Công nghệ Giao thông vận tải Người phản biện: GS. TSKH. Hà Huy Cương TS. Nguyễn Minh Khoa |
Tóm tắt: Bài báo trình bày phương pháp sử dụng nội lực (mô men uốn Mx, My, mô men xoắn Mxy, lực cắt Qx, Qy) làm ẩn và nguyên lý năng lượng biến dạng đàn hồi tối thiểu để xây dựng bài toán tấm chịu uốn khi có xét biến dạng trượt ngang, sau đó đưa ra một ví dụ lời giải số và so sánh kết quả với lời giải giải tích.
Từ khóa: Biến dạng đàn hồi, tấm chịu uốn, trượt ngang.
Abstract: This paper presents a method of using the internal forces (bending, torque, shear) are unknown and minimum deformation energy principle in elastic for the effect of transverse shear deformation on the bending of elastic plates. Then we give an example of numerical solution and compare the results with analytical solutions.
Keywords: Elastic deformation, bendable plate, horizontal sliding.
1. Đặt vấn đề
Phương pháp phần tử hữu hạn (PTHH) là phương pháp chuyển vị được sử dụng rộng rãi hiện nay trong phân tích đàn hồi, đàn dẻo, dẻo và thiết kế tối ưu công trình. Tuy nhiên, sử dụng ứng suất hoặc nội lực làm ẩn cũng rất thuận tiện trong phân tích đàn hồi và đặc biệt là khi phân tích giới hạn (Limit Analysis) theo định lý giới hạn dưới. Bài báo trình bày phương pháp sử dụng phương trình cân bằng lực và nguyên lý năng lượng đàn hồi tối thiểu để xây dựng bài toán tấm chịu uốn có xét biến dạng trượt ngang sử dụng nội lực làm ẩn.
2. Lý thuyết tấm chịu uốn có xét biến dạng trượt ngang
Xét tấm chữ nhật có chiều dày h không đổi trên toàn bộ diện tích. Vật liệu của tấm đàn hồi tuân theo định luật Hook. Gọi mặt trung bình là mặt phẳng song song với mặt trên, mặt dưới và đi qua điểm chính giữa theo chiều dày tấm.
Lý thuyết tấm mỏng chịu uốn (lý thuyết tấm Kirchhoff) sử dụng 3 giả thiết [2],[3]:
- Tại mặt phẳng trung bình, tấm không bị biến dạng và do đó không có ứng suất trong mặt phẳng của nó, vì thế khi tấm chịu uốn nó còn được gọi là mặt trung hòa;
- Tiết diện phẳng thẳng góc với mặt trung bình trước khi biến dạng thì sau khi biến dạng vẫn phẳng và thẳng góc với mặt trung bình;
- Không xét ảnh hưởng của ứng suất pháp tác dụng lên các mặt song song với mặt trung bình.
Tuy nhiên, khi tính tấm có xét biến dạng trượt ngang thì giả thiết 2 có thay đổi đó là tiết diện phẳng thẳng góc với mặt trung bình trước khi biến dạng thì sau khi biến dạng vẫn phẳng nhưng không thẳng góc với mặt trung bình. Nhờ các giả thiết của lý thuyết tấm chịu uốn ta chỉ cần xét mặt trung hòa có độ võng w(x,y) và các mô men, các lực cắt tác dụng lên nó.
Hiện nay, người ta thường sử dụng lý thuyết xét biến dạng trượt ngang trong tấm của Reissner [2,3], lý thuyết tấm dày Mindlin [2] và lý thuyết dầm Timôsenkô [2]. Theo lý thuyết dầm Timôsenkô[2], các góc xoay φx, φy, các biến dạng uốn xx xy xxy (các độ cong) của tấm và các mô men nội lực Mx, My, Mxy được xác định như sau [1,trang 37]:
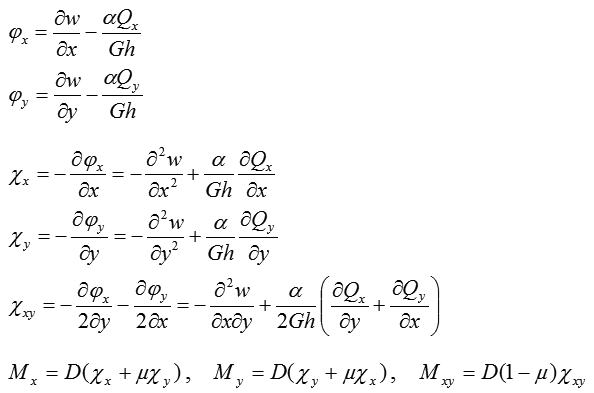 |
(1)
(2)
(3)
Trong đó:
α - Hệ số xét đến sự phân bố không đều của ứng suất cắt trên tiết diện khi xét ảnh hưởng của biến dạng trượt ngang, với dầm có tiết diện chữ nhật đặc, ta có α =1,2;
μ - Hệ số Poisson của vật liệu;
G - Mô đun đàn hồi trượt của vật liệu.
Thay (2) vào (3) ta được:
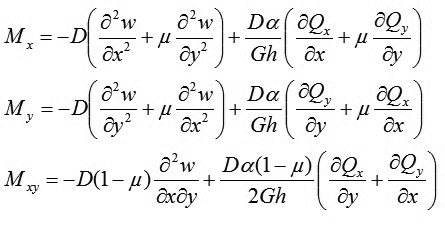 |
(4)
Với D - Độ cứng trụ của tấm,
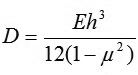 |
E - Mô đun đàn hồi kéo (nén) của vật liệu. Lý thuyết tấm xét biến dạng trượt ngang như trình bày ở trên xem các hàm độ võng w, hàm lực cắt Qx và hàm lực cắt Qy là những hàm ẩn độc lập.
Ta thấy các thành phần thứ 2 trong các công thức (4) là các thành phần xét biến dạng trượt ngang. Thay G∞ hoặc h0 vào (4) ta lại nhận được các công thức xác định mô men uốn và mô men xoắn của lý thuyết tấm thông thường.
Mặt khác, xét một phân tố chữ nhật có các cạnh dx, dy tách ra từ mặt trung hòa, chịu tác dụng của lực q (Hình 2.1). Tác dụng lên phân tố là các mô men uốn Mx, My; mô men xoắn Mxy; lực cắt Qx, Qy (Xét trong tọa độ Đề các)
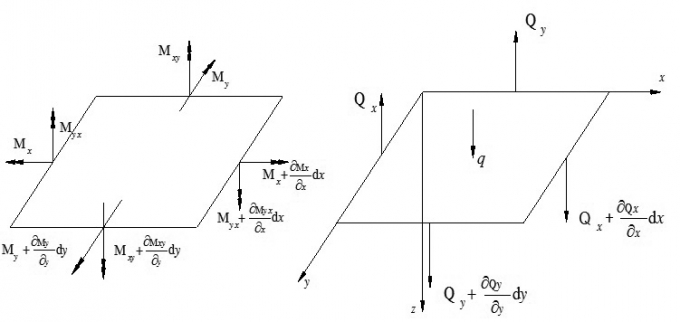 |
| Hình 2.1: Các nội lực tác dụng lên phân tố tại mặt trung hòa |
Xét cân bằng phân tố cho ta các phương trình cân bằng sau:
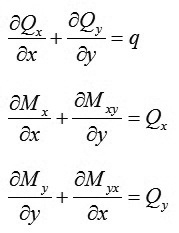 |
(5a)
(5b)
(5c)
Hoặc có thể viết:
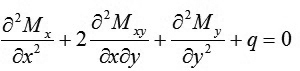 |
(5d)
Thay (4) vào (5b), (5c) rồi biến đổi ta được:
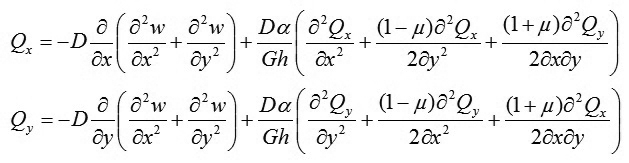 |
(6)
Đưa (4) vào phương trình (5d) ta được phương trình vi phân độ võng tấm:
(7)
Tóm lại, bằng phương pháp cân bằng phân tố, tác giả xây dựng được hệ phương trình (1), kết hợp với lý thuyết tấm chịu uốn có xét biến dạng trượt ngang hiện nay cũng như các điều kiện biên của tấm theo chiều x,y ta xác định được các ẩn nội lực Mx, My, Mxy, Qx, Qy và độ võng w như hệ phương trình (2). Nếu lý thuyết tấm thông thường chỉ cho phép thỏa mãn 2 điều kiện biên trên mỗi cạnh tấm thì lý thuyết tấm có xét biến dạng trượt ngang như đã trình bày ở trên cho phép thỏa mãn 3 điều kiện biên trên mỗi cạnh tấm (thêm điều kiện mô men xoắn Mxy=0).
3. Bài toán phân tích đàn hồi tấm chịu uốn có xét biến dạng trượt ngang sử dụng nội lực làm ẩn
Thông thường người ta sử dụng phương pháp PTHH (phương pháp chuyển vị) để giải bài toán tấm nhưng ở đây ta sử dụng nội lực làm ẩn nên khi phân tích đàn hồi tấm có xét biến dạng trượt ngang ta có 5 hàm ẩn là 3 mô men nội lực Mx(x,y), My(x,y), Mxy(x,y) và 2 hàm ẩn lực cắt Qx(x,y), Qy(x,y). Trong đó: (x,y) - Tọa độ của điểm trong mặt trung bình của tấm. Vì vậy, bài toán phân tích đàn hồi tấm có xét biến dạng trượt ngang có thể giải bằng cách tìm min của năng lượng biến dạng đàn hồi (NLBDĐH) với điều kiện ràng buộc là ba phương trình (5b)(5c)(5d):
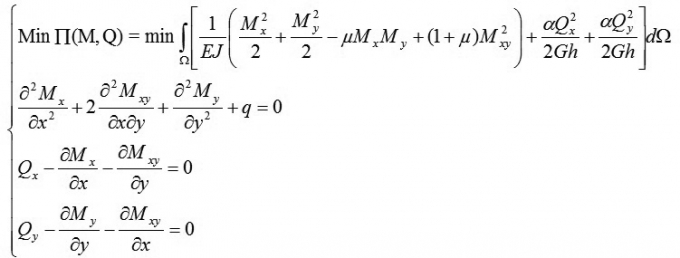 |
(8)
Bài toán (8) là bài toán tối ưu có ràng buộc, để giải bài toán này có thể đưa (8) về bài toán không có điều kiện ràng buộc bằng cách viết phiếm hàm Lagrange mở rộng sau:
 |
(9)
Trong đó: λ= λ(x,y) ; λ1= λ1(x,y) và λ2= λ2(x,y) - Thừa số Lagrange và cũng chính là các hàm ẩn cần xác định; Ω - Diện tích tấm. Phiếm hàm F có 8 ẩn và hàm ẩn cần xác định là: Mx ; My; Mxy ; Qx ; Qy ; λ; λ1 và λ2. Sử dụng phép tính biến phân đối với phiếm hàm (9) ta nhận được 8 phương trình Euler- Lagrange như sau:
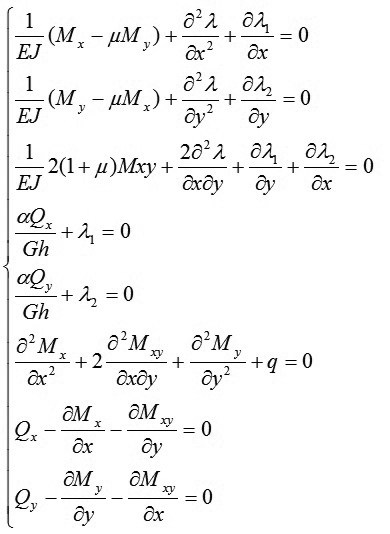 |
(10)
Rút λ1, λ2 từ phương trình thứ 4, thứ 5 rồi thay vào 3 phương trình đầu thì 5 phương trình đầu của (10) chỉ còn lại 3 phương trình sau:
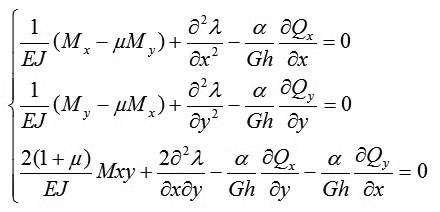 |
(11)
Nhận thấy λ trong hệ phương trình (11) có thứ nguyên là chuyển vị và đó chính là độ võng w(x,y) của mặt trung bình tấm. Thay λ= w vào (11) rồi biến đổi các phương trình của (11) ta được:
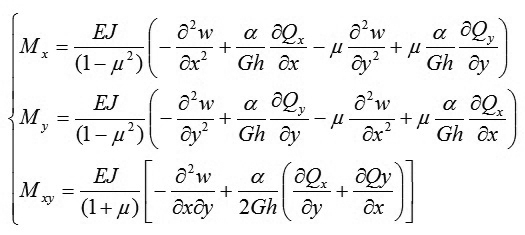 |
(12)
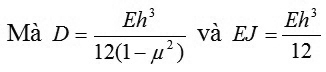 |
(lấy b=1) nên suy ra
Thay vào (12) và viết gọn lại ta được:
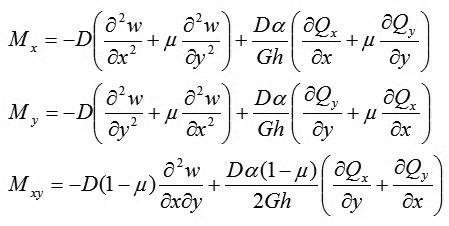 |
(13)
Đưa (13) vào hai phương trình cuối của (10) và biến đổi ta xác định:
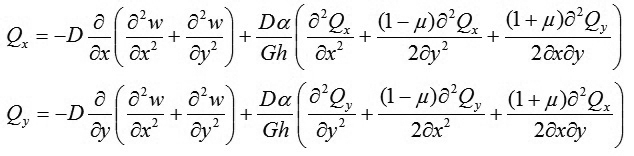 |
(14)
Vậy, từ 5 phương trình đầu và 2 phương trình cuối của (10) ta rút ra được (13) và (14), kết hợp với phương trình còn lại (phương trình thứ 6) của hệ (10) khi đó hệ phương trình (10) sẽ tương đương với hệ phương trình sau:
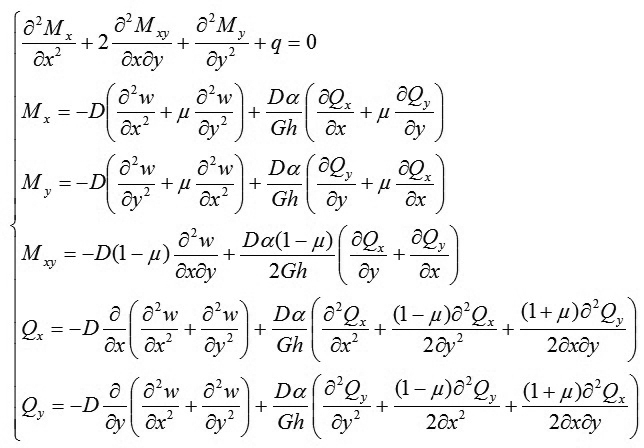 |
(15)
Giải hệ phương trình (15) cùng với các điều kiện biên về nội lực và chuyển vị của tấm ta sẽ xác định được 6 ẩn chưa biết Mx ; My; Mxy , Qx ; Qy và w.
Tóm lại, bằng cách sử dụng phép tính biến phân ta đã dẫn bài toán cực trị (8) về giải hệ phương trình vi phân (15). Ta nói bài toán cực trị (8) tương đương với hệ phương trình (15).
Bài toán (8) khi rời rạc hóa sẽ là bài toán của toán học tối ưu (bài toán vận trù học, quy hoạch toán) với ẩn là các tham số. Bài toán này có hàm mục tiêu ở dạng bậc 2 và các điều kiện ràng buộc là các phương trình tuyến tính. Các phương pháp quy hoạch toán (bài toán tối ưu) phát triển rất mạnh mẽ đến mức có nhiều chương trình viết sẵn để giải các bài toán này kể cả các bài toán tối ưu phức tạp như hàm mục tiêu là dạng phi tuyến bất kỳ, các ràng buộc là phi tuyến hoặc tuyến tính, phương trình hoặc bất đẳng thức. Người kỹ sư có thể sử dụng các chương trình này như sử dụng chương trình giải hệ phương trình bậc nhất, các chương trình về tính đại số ma trận… (ví dụ các chương trình tối ưu của Matlab).
4. Lời giải số
Tác giả trình bày một ví dụ về tính tấm chữ nhật tựa khớp ở chu vi, chịu tải trọng phân bố q. Như đã trình bày ở trên, để phân tích đàn hồi tấm có xét biến dạng trượt ngang ta có thể giải bài toán (8) hoặc giải hệ (15). Ở đây, tác giả giải trực tiếp bài toán tối ưu (8). Do phương trình cân bằng dùng ẩn là nội lực nên ở đây tác giả sử dụng phương pháp rời rạc hóa bằng sai phân hữu hạn. Trường hợp cần xác định chuyển vị (độ võng w của tấm) thì ta đưa thêm 3 phương trình (13) vào bài toán và sử dụng các hàm nội suy của phương pháp PTHH để giải.
Xét tấm chữ nhật có kích thước axb, chia tấm thành nxm phần tử, tại mỗi nút của phần tử sẽ có các ẩn là Mx ; My; Mxy ; Qx ; Qy . Trong bài toán này tác giả chỉ sử dụng lý thuyết 2 điều kiện biên (không thỏa mãn điều kiện mô men xoắn Mxy=0 trên các biên tấm). Điều kiện biên trên mỗi cạnh tấm như sau:
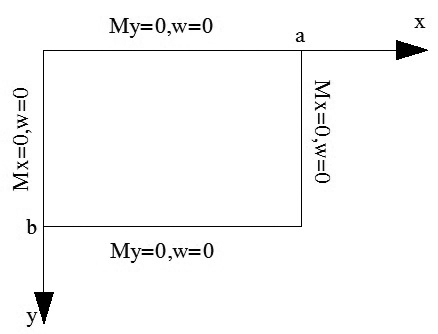 |
| Hình 4.1: Điều kiện biên của tấm tựa khớp |
Để giải bài toán này, tác giả viết chương trình trong môi trường Matlab. Chia tấm thành mxn phần tử, kết hợp với các điều kiện biên trên cạnh khớp xác định được toàn bộ số ẩn của tấm.
Kết quả tính độ võng và mô men uốn tại điểm giữa tấm với các trường hợp tỷ lệ chiều dày tấm so với cạnh tấm (h/a) thay đổi thể hiện ở Bảng 4.1:
Bảng 4.1. Tấm chữ nhật tựa khớp chịu tác dụng của tải trọng phân bố đều có xét ảnh hưởng của biến dạng trượt ngang, hệ số Poisson của vật liệu μ=0,3
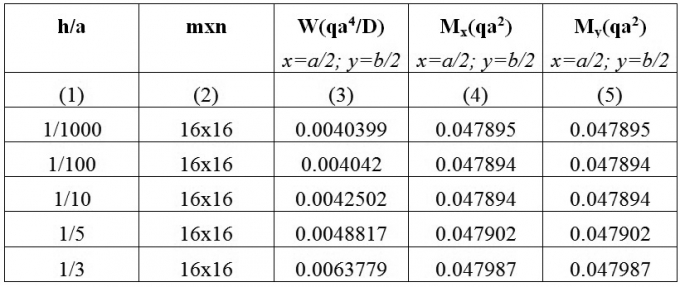 |
Kết quả ở cột (3) (4) (5) là độ võng W, mô men uốn Mx , My tại điểm giữa tấm khi xét đến ảnh hưởng của biến dạng trượt ngang. Từ kết quả trên ta thấy, trường hợp h/a =1/1000 hoặc h/a = 1/100 thì nhận được độ võng xấp xỉ với độ võng theo lý thuyết tấm thông thường (so với lời giải giải tích của Timôsenkô Wmax=0,00406 qa4/D thì sai số là < 0,5%). Khi tỷ lệ h/a thay đổi thì ảnh hưởng của biến dạng trượt ngang đến độ võng thay đổi đáng kể. Theo kết quả ở Bảng 4.1, khi h/a =1/5 thì độ võng tăng lên khoảng 20%, khi h/a =1/3 thì độ võng tăng lên khoảng 50% so với độ võng khi tính theo lý thuyết tấm thông thường.
Biểu đồ độ võng, sự biến thiên của nội lực mô men uốn, mô men xoắn của tấm chịu uốn có xét ảnh hưởng của biến dạng trượt ngang (trong trường hợp chia tấm thành 16x16 phần tử, tỷ lệ h/a =1/5) như Hình 4.2.
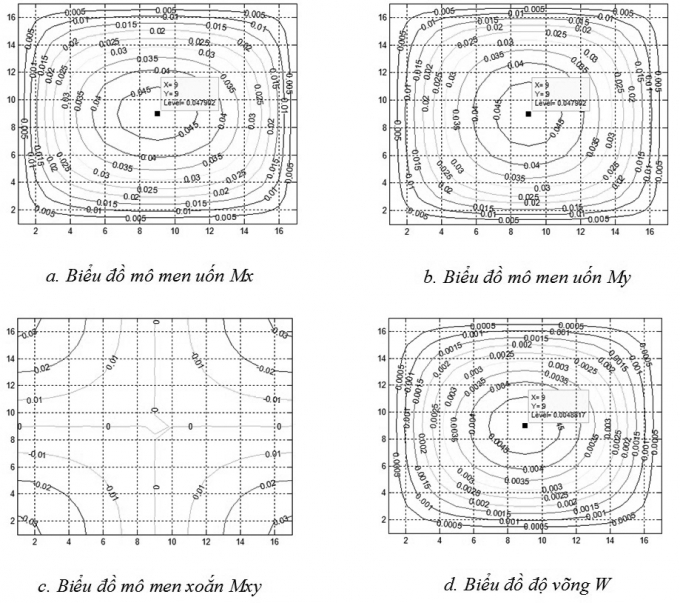 |
| Hình 4.2: Kết quả tính toán |
Chú ý: Phương pháp trên tác giả dùng để tính phân tích Limit của tấm sau này.
Tài liệu tham khảo
[1]. N.I.Bêdukhốp (1978), Cơ sở lý thuyết đàn hồi, lý thuyết dẻo, lý thuyết từ biến, Người dịch: Phan Ngọc Châu. NXB. Đại học và trung học chuyên nghiệp, Hà Nội.
[2]. X.P.Timôsenkô - X.Vôinôpxki - Krige (1971), Tấm và vỏ, Người dịch: Phạm Hồng Giang, Vũ Thành Hải, Đoàn Hữu Quang. NXB. Khoa học và kỹ thuật, Hà Nội.
[3]. Nguyễn Thùy Anh (2011), Phương pháp mới tính tấm chữ nhật chịu uốn, Luận án tiến sĩ.
Tag:





Bình luận
Thông báo
Bạn đã gửi thành công.